I hope this huge list will be helpful to you. If you like any of the cheatsheet whether it will be machine learning algorithms cheat sheet or scikit-learn cheat sheet or data visualization cheat sheet or keras cheat sheet or tensorflow cheat sheet or any other cheatsheets, then please share this list with others, so they can also use this in machine learning or data science task. Gear up to speed and have concepts and commands handy in Data Science, Data Mining, and Machine learning algorithms with these cheat sheets covering R, Python, Django, MySQL, SQL, Hadoop, Apache Spark, Matlab, and Java. Jupyter Notebook is a web-based interface that helps you to build and exchange documents containing live code, visualizations, informative text, and equations. Also, Jupyter Notebook includes statistical modeling, numerical simulation, machine learning, data cleaning, and transformation. In this cheat sheet you will learn the following techniques.

• Cheat Sheet For Machine Learning Algorithms
• Machine Learning Algorithms Cheat Sheet Free
• Machine Learning Algorithms Cheat Sheet R
• Machine Learning Algorithms Cheat Sheet 5th
• Machine Learning Algorithms Cheat Sheet Pdf
• Full Cheat Sheet On Machine Learning Algorithms In Python And R Pdf

Cheat Sheet For Machine Learning Algorithms

A cheat sheet

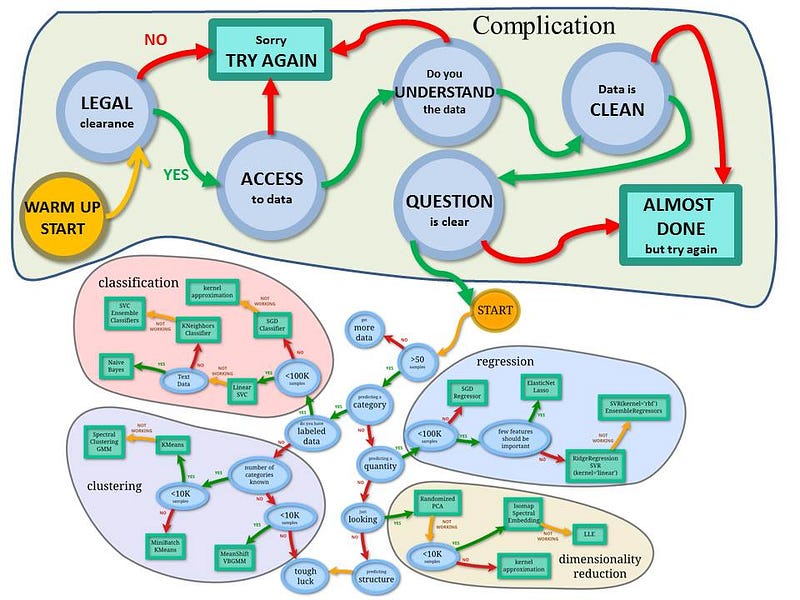
Scikit Learn Cheat Sheet Scikit-learn is a free software machine learning library for the Python programming language. It features various classification, regression and clustering algorithms including support vector machines is a simple and efficient tools for data mining and data analysis. The Azure Machine Learning Algorithm Cheat Sheet helps you choose the right algorithm from the designer for a predictive analytics model. Azure Machine Learning has a large library of algorithms from the classification, recommender systems, clustering, anomaly detection, regression, and text analytics families.

This cheatsheet wants to provide an overview of the concepts and the used formulas and definitions of the »Machine Learning«online course at coursera.

Please note: I changed the notation very slighty. I'll denote vectors with a little arrow on the top. Example: $vectheta$

The octave tutorial that was part of the seond week is available as a script here.

Week 1

Introduction

Machine Learning

»Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure E, if its performance on T, as measured by P, improves with experience E.«
— Tom Mitchell (1998)^[1]

Supervised Learning

Supervised learning is the task of learning to predict the answers for unseen examples where the right answers for some examples are given to learn from.

Unsupervised Learning

Unsupervised learning is learning in the absence of right answers to learn from. The algorithm discovers structure in the data on its own.

Regression Problem

Regression problems need estimators to predict continuous output, such as house prices.

Classification Problem

Classification problems need estimators to predict categorical (discrete) valued output. (I.e. $0$ or $1$, whether or not a patient has cancer or not.)

Linear Regression with One Variable

Model Representation

Notations:

• $m$: number of training examples
• $x$'s: input variable/features
• $y$'s: output variables/target
• $(x,y)$: one training example
• $(x^{(i)},y^{(i)})$: $i$^th training example

Univariate Hypothesis

The hypothesis function maps x's to y's ($h: x mapsto y$). It can be represented by:

$$h_{theta} = theta_{0} + theta_{1}x$$

The shorthand for the hypothesis is $h(x)$. $theta_{i}$'s are called the parameters of the hypothesis. In this case the hypothesis is called »Univariate Linear Regression«.

Cost Function

Idea: Choose $theta_0, theta_1$ so that $h_theta(x)$ is close to $y$ for our training examples $(x,y)$. The 3D-surface plot below visualizes the cost function for the two parameters.

Squared Error Cost Function

$$J(theta_0, theta_1) = frac{1}{2m} sum^{m}_{i=1}left(h_{theta}(x^{(i)}) - y^{(i)}right)^2$$

The Gradient Descent Algorithm

The goal is to choose the hypothises' parameters in a manner that the the output of the cost function $J(theta_0, theta_1)$ is minimal.

Outline:

• Start with some $theta_0, theta_1$
• Keep changing $theta_0, theta_1$ to reduce $J(theta_0, theta_1)$ until we hopefully end up at a minimum

Gradient Descent Algorithm

Note that the values of $theta_0$ and $theta_1$ are updated simultaneously. $alpha$ is called the learning rate.

$$begin{aligned} text{repeat} & text{ until convergence} ; { & theta_j := theta_j - alpha frac{delta}{deltatheta_j} J(theta_0, theta_1) ;; text{(for j=0 and j=1)} } phantom{15pt} & end{aligned}$$

The correct implementation of the simultaneous update looks like this:

$$begin{aligned} & temp0 := theta_0 - alpha frac{delta}{deltatheta_j} J(theta_0, theta_1) & temp1 := theta_1 - alpha frac{delta}{deltatheta_j} J(theta_0, theta_1) & theta_0 := temp0 & theta_1 := temp1 end{aligned}$$

Partial derivitive of the cost function

$$begin{aligned} text{repeat} & text{ until convergence} ; { & theta_0 := theta_0 - alpha frac{1}{m} sum^{m}_{i=0}left(h_theta(x^{(i)}) - y^{(i)}right) & theta_1 := theta_1 - alpha frac{1}{m} sum^{m}_{i=0}left(h_theta(x^{(i)}) - y^{(i)}right) cdot x^{(i)} } phantom{15pt} & end{aligned}$$

Note: The cost function $J(theta_0, theta_1)$ is convex and therefore has only one optimum overall.

Batch Gradient Descent

If the gradient descent uses all $m$ training examples in each iteration it is also called Batch Gradient Descent Algorithm.

Week 2

Linear Regression with Multiple Variables

Multiple Features

Notations:

• $n$: number of features
• $vec x^{(i)}$: input features of i^th training example
• $x^{(i)}_j$: value of feature $j$ in i^th training example

Multivariate Hypothesis

$$h_theta = theta_0 + theta_1 x_1 + theta_2 x_2 + cdots + theta_n x_n$$

For convenience of notation we'll define $x_0 = 1$ ($x_0^{(i)}$). Thus a feature vector looks like:

$$ vec x = left[begin{array}{c} x_0 x_1 vdots x_n end{array}right] in mathbb{R}^{n+1}$$

And the parameters can be written as:

$$ vec theta = left[begin{array}{c} theta_0 theta_1 vdots theta_n end{array}right] in mathbb{R}^{n+1}$$

The hypothesis can now be written as:

$$begin{align} h_theta & = theta_0 x_0 + theta_1 x_1 + theta_2 x_2 + cdots + theta_n x_n & = left[ theta_0 theta_1 cdots theta_n right] left[begin{array}{c} theta_0 theta_1 vdots theta_n end{array}right] & = boxed{vectheta^{T}vec x} end{align}$$

This hypothesis is called »Multivariate Linear Regression«.

Gradient Descent for Multiple Variables

The cost function can now be written as:

$$begin{aligned} J(theta_0, theta_1, ..., theta_n) & = frac{1}{2m}sum^{m}_{i=1} left(h_theta(x^{(i)}) - y^{(i)}right)^2 & = boxed{J(vectheta)} end{aligned}$$

The gradient descent algorithm for this cost function looks like this:

$$begin{aligned} text{repeat} & { & theta_j := theta_j - alpha frac{delta}{delta theta_j} ; ; J(theta_0, theta_1, ... , theta_n) } phantom{15pt} & end{aligned}$$

Which can also be written like this:

$$begin{aligned} text{repeat} & { & theta_j := theta_j - alpha frac{1}{m} sum^{m}_{i=1}left( h_theta(vec x^{(i)}) -y^{(i)} right) x_j^{(i)}) } phantom{15pt} & end{aligned}$$

Again, the parameters $theta_j ; forall j= 0, ..., n$ have to be updated simultaneously.

Feature Scaling

Get every feature into approximately a $-1 leq x_i leq 1$ range to optimize the path finding of the gradient descent algorithm.

Mean Normalization

Replace $x_i$ with $x_i - mu_i$ to make features have approximately zero mean (does not apply to $x_0 = 1$).

$$x_1 leftarrow frac{x_1 - mu_1}{s_1}$$

where $mu_1$ is the average value of x in the training set and $s_1$ is the range $max - min$ (or standard deviation).

Learning Rate $alpha$

General rule: $J(vectheta)$ should decrease after every iteration.

Example Automatic Convergence Test

Declare convergence if $J(vectheta)$ decreases by less than $epsilon = 10^{-3}$ in one iteration.

Make sure gradient descent works correctly:

• If $alpha$ is too small: slow convergence
• If $alpha$ is too large: $J(vectheta)$ may not decrease on every iteration and may not converge

For $alpha$ try: $0.001$, $0.003$, $0.01$, $0.03$, $0.1$, $0.3$, $1$ etc.

Features and Polynomial Regression

You can choose your model to fit to a polynomial if you want it to behave in a specific way. You not only can choose to multiply/divide two or more features to create a new feature, you can also fit your model to a more complex polynomial. If you want your model to behave for example to increase you could choose to use $(size)^2$, fit it to a cubic polynomial the same way, or use $sqrt{size}$.

Normal Equation

An alternative to the gradient descent algorithm is an analytical solution to minimize the cost function $J(vectheta)$.

$$theta in mathbb{R}^{n+1} ;;; J(theta_0, theta_1, cdots, theta_m) = frac{1}{2m}sum^{m}_{i=1} left( h_theta(x^{(i)} - y^{(i)}right)^2$$ $$frac{delta}{deltatheta_j} J(vectheta) = cdots = 0 ;;; text{(for every $j$)}$$

Then solve for $theta_0,theta_1,cdots,theta_n$ by setting the equation to equal zero. For $m$ examples $(vec x^{(i)}, y^{(i)}), cdots, (vec x^{(m)}, y^{(m)})$ with $n$ features the input feature of the i^th training example looks like this:

$$vec x^{(i)} = left[ begin{array}{c} x_0^{(i)} x_1^{(i)} vdots x_n^{(i)} end{array} right] in mathbb{R}^{n+1}$$

The design matrix $x$ then looks like that:

$$ X = left[ begin{array}{c} (x^{(1)})^T (x^{(2)})^T vdots (x^{(m)})^T end{array} right]$$

and the vector of the outputs of the training examples look like this:

$$ vec y = left[ begin{array}{c} y^{(1)} y^{(2)} vdots y^{(m)}end{array}right]$$

With the design matrix the minimum $vec theta$ is:

$$ vec theta = (X^TX)^{-1} X^T vec y$$

Note: using this method you don't need to scale the features.

Gradient Descent versus Normal Equation

For $m$ training examples and $n$ features:

Gradient Descent:

• Need to choose $alpha$
• Needs many iterations
• Works well even when $n$ is large

Normal Equation

• No need to choose $alpha$
• Don't need to iterate
• Need to compute $(X^TX)^{-1})$ (complexity $O(n^3)$)
• Slow if $n$ is very large

Normal Equation Noninvertibility

Although very rarely, it can happen that $X^TX$ is non-invertible, for example if the matrix is singular or degenerate.

Problems can be that redundant features are used (and therefore the vetors are linearly dependent) or that too many features are used (e.g. $m leq n$). The solution for that would be to delete some features or use regularization (which comes later in this course).

Week 3

Linear Regression

With $y in {0, 1}$ the linear regression model is

$$0 leq h_theta(x) leq 1$$

Hypothesis for Logistic Regression Models

The hypothesis for this model is this:

$$h_theta(x) = g(theta^Tx)$$

Where $g$ is called sigmoid function or logistic function

$$g(z) = frac{1}{1+e^{-z}}$$

Which gives us the following representation for the hypothesis:

$$h_theta(x) = frac{1}{1+e^{-theta^Tx}}$$

Interpretation of the Hypothesis Output

$h_theta(x)$ is the estimated probability that $y=1$ on input $x$:

$$h_theta(x) = P(y = 1 | x ; theta)$$

Which reads like probability that $y=1$ given x, parameterized by $theta$

$$P(y=0|x;theta) + P(y=1|x;theta) = 1 P(y=0|x;theta) = 1 - P(y=1|x;theta)$$

Decision Boundary

Suppose we predict $y=1$ if $h_theta(x) geq 0.5$. $g(z) geq 0.5 $ when $z geq 0$. For $h_theta(x) = g(theta^Tx) geq 0.5$ whenever $z = theta^Tx geq 0$. Suppose we predict $y=0$ if $h_theta(x) < 0.5$.

The decision boundary ist part of the hypothesis. If we for example have a hypothesis with two features, the term $theta_0 + theta_1 x_1 + theta_2 x_2$ gives the decision boundary, where this is the hypothesis:

$$h_theta(x) = g(theta_0 + theta_1 x_1 + theta_2 x_2)$$

Non-linear Decision Boundaries

As previously mentioned one can add custom features to fit the hypothesis to the data. This allows us to add custom features that result in a circular decision boundary.

For example:

$$vec theta = left[begin{array}{c} -1 0 0 1 1 end{array}right]$$

With custom features $x_1^2$ and $x_2^2$:

$$h_theta(x) = theta_0 + theta_1 x_1 + theta_2 x_2 + theta_3 x_1^2 + theta_4 x_2^2$$

We predict $y=1$ if $-1 + x^2_1 + x^2_2 geq 0$. The polynom can have as much custom features as you wish to fit the data. Even with non-circular non-linear decision boundaries.

Cost Function

Notation:

• Training set: $left{ (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), cdots, (x^{(m)}, y^{(m)})right}$
• $m$ examples $;;;x in left[begin{array}{c} x_0 x_1 vdots x_n end{array}right] ; ; ; x_0 = 1, y in {0,1}$
• $h_theta = frac{1}{1+e^{-theta^Tx}}$

The cost function for linear regression was:

$$J(vectheta) = frac{1}{m} sum^m_{i=1} frac{1}{2}left(h_theta(x^{(i)}) - y^{(i)}right)^2 = cost(h_theta(x^{(i)}), y^{(i)}) cost(h_theta(vec x), vec y) = frac{1}{2}(h_theta(vec x) - vec y)^2$$

This cost function is non-convex. For logistic regression we want a convex function.

$$cost(h_theta(vec x), vec y) = left{ begin{array}{r} -log(h_theta(vec x)) ;;; text{if} ;; y = 1 -log(1 - h_theta(vec x)) ;;; text{if} ;; y = 0end{array}right.$$

If the $text{cost} , = 0 ; text{if} ; y = 1, h_theta(x) = 1$ but as $h_theta(x) rightarrow 0$ $Cost rightarrow infty$. This captures the intuition that if $h_theta(x) = 0$ (predict $P(y=1|x;theta)$), but $y=1$ we'll penalize the learning alrogithm by a very large cost.

Simplified Cost Function and Gradient Descent

The cost function can be simplified to a one liner:

$$cost(h_theta(x),x) = -y ; log(h_theta(x)) - (1-y) log(1-h_theta(x))$$

This works because if $y=1$, the first term will be multiplicated by $1$ and the second term will be multiplicated with $(1-y) = (1-1) = 0$. If $y=0$ the first term is multiplicated with 0 and the second term is multiplicated with $(1-0) = 1$.

This gives us the complete cost function $J(vectheta)$:

$$begin{align} J(vectheta) & = frac{1}{m} sum^m_{i=1} cost(h_theta(x^{(i)}),y^{(i)}) & = - frac{1}{m} left[sum^m_{i=1} y^{(i)} log(h_theta(x^{(i)})) + (1-y^{(i)} ) log(1 - h_theta( x^{(i)}))right] end{align}$$

To fit parameters $vectheta$ $text{min}_theta J(vectheta)$ is calculated. To make a new prediction given new x the output of $h_theta$ has to be calculated ($P(y=1|x;theta)$).

Gradient Descent

$text{min}_theta J(theta)$:

$$begin{aligned} text{repeat} &{ & theta_j := theta_j - alpha sum^m_{i=1} (h_theta(x^{(i)}) - y^{(i)})x_j^{(i)} } phantom{15pt} & end{aligned}$$

Advanced Optimization

In general we need to compute two things for our optimization:

• $J(vec theta)$
• $frac{delta}{deltatheta_j}J(vec theta)$

Besides gradient descent, there are several other algorithms that could be used:

• Conjugate Gradient
• BFGS
• L-BFGS

The advantages:

• No need to manually pick $alpha$
• Often faster than gradient descent

The disadvantages:

• More complex

Example for $text{min}_theta$

$$vectheta=left[begin{array}{c} theta_1 theta_2 end{array}right] J(vectheta) = (theta_1 -5)^2 + (theta_2 -5)^2 frac{delta}{deltatheta_1}=2(theta_1 -5) frac{delta}{deltatheta_2} = 2(theta_2 - 5)$$

Multiclass Classification: One-vs-all

Classification with more than two $y$'s works like this:

$$h_theta^{(i)}(x) = P(y=i|x;theta) ;;; (i = 1,2,3,...)$$

Each $i$ has it's own hypothesis $h_theta^{(i)}(x)$ and predicts the probability that $y=i$ for each class $i$. On a new input $x$, to make a prediction, pick the class $i$ that maximizes $text{max}_i h_theta^{(i)}(x)$

Regularization

To prevent overfitting or underfitting of our hypothesis, we can regularize regressions.

Regularized Linear Regression

$$J(vectheta) = frac{1}{2m} left[sum^m_{i=1}(h_theta(x^{(i)}) -y^{(i)})^2 + lambda sum^m_{j=1}theta_j right]$$

Where the term prepended by $y$ is called the regularization term. The goal is again to $text{min}_theta ; J(vectheta)$. The regularized gradient descent looks like this:

$$begin{aligned} text{repeat} & { & theta_0 := theta_0 - alpha frac{1}{m} sum^m_{i=0} (h_theta(x^{(i)}) - y^{(i)})x_0^{(i)} & theta_j := theta_j - alpha left[ frac{1}{m} sum^m_{i=0} (h_theta(x^{(i)}) - y^{(i)})x^{(i)}_j + frac{lambda}{m} theta_j right] ;; text{(for j=1...n)} } phantom{15pt} & end{aligned}$$

Note that $theta_0$ does not get penalized for over- or underfitting and therefore not regularized. The second term simply is $frac{delta}{delta theta_j} J(vectheta)$. For $j > 0$ the term can also be written as:

$$theta_j = theta_j(1-alpha frac{lambda}{m}) - alpha frac{1}{m} sum^m_{i=0}(h_theta(x^{(i)}) - y^{(i)})x^{(i)}_j$$

You can see that written this way, the term is pretty much the same as the original term.

Regularized Normal Equation

$$X = left[begin{array}{c} (x^{(1)})^T vdots (x^{(m)})^T end{array}right] in mathbb{R}^{mx(n+1)} ;; text{with} ;; y = left[begin{array}{c} y^{(1)} vdots y^{(m)} end{array}right] in mathbb{R}^{m}$$

The regularized normal equation now looks like this:

$$vectheta = (X^T X + lambda left[begin{array}{ccccc} 0 & 0 & 0 & cdots & 0 0 & 1 & 0 & cdots & 0 0 & 0 & 1 & cdots & 0 vdots & vdots & vdots & ddots & vdots 0 & 0 & 0 & cdots & 1 end{array}right])^{-1}X^T y$$

Where the matrix consisting of zeros and ones is sized $(n+1)x(n+1)$.

Non-Invertibility

Suppose $m leq n$ where $m$ is the number of examples and $n$ is the number of features.

$$theta = (X^TX)^{-1}X^T y$$

When $m leq n$ $X^TX$ is not invertible.

If $lambda > 0$ the matrix is invertible because of the regularization.

Regularized Logistic Regression

$$J(vec theta) = - left[ frac{1}{m} sum^{m}_{i=1} log(h_theta(x^{(i)})) + (1-y^{(i)})log(1- h_theta(x^{(i)})) right] + frac{lambda}{2m} sum^m_{i=1} theta^2_j$$

To prevent overfitting, $theta_j$ will be penalized with $y>0$ for being too large.

Week 4

Neural Networks: Representation

Non-Linear Hypothesis

For more complex hypothesis that are non-linear to fit the hypothesis it might be required to add a number of quadratic or other features. With a higher number of features, this results in a really large hypothesis. This is where neural networks come in.

Model Representation I

• Dendrite: input wires
• Axon: output wire

• Hypothesis: $h_Theta(x) = frac{1}{1+e^{-Theta^Tx}}$ (also called sigmoid activation function)
• $x_0$: bias unit with $x_0 = 1$

The so called weights of the neurons are going to be the parameters of this model.

Again, $x_0$ and $a_0^(2)$ are the bias units. The first layer (${x_0, x_1, x_2, x_3}$) is called the input layer. The third layer (${a^{(2)}_0, a^{(2)}_1, a^{(2)}_2, a^{(2)}_3}$) is called the output layer. All layers between the input and the output layers are called hidden layers. So in this example, layer 2 is a hidden layer.

• $a^{(j)}_i$: activation of unit $i$ in layer $j$
• $Theta^{(j)}$: matrix of weights controlling function mapping from layer $j$ to layer $j+1$

In general, if a network has $s_j$ units in layer $j$, $s_{j+1}$ units in layer $j+1$, then $Theta^{(j)}$ will be of dimension $s_{j+1} times (s_j+1)$

Model Representation II

Forward Propagation: Vectorized Implementation

From the first layer to the output layer the values are calculated based on the values of the previous layer.

$$x=left[begin{array}{c} x_0 vdots x_3 end{array}right], ;; z^{(2)}=left[begin{array}{c} z^{(2)}_1 z^{(2)}_2 z^{(2)}_3 end{array}right]$$

With $z^{(2)} = Theta^{(1)}a^{(1)}$ and $a^{(2)} = g(z^{(3)})$. Basically this is just a logistic regression for each layer $a_i^{(j)}$. For the bias unit we add $a^{(2)}_0 = 1$ ($Rightarrow a^{(2)} in mathbb{R}^{n+1}$). $z^{(3)} = Theta^{(2)}a^{(2)}$ and $h_Theta(x) = a^{(3)} = g(z^{(3)})$.

Examples and Intuitition I

Simple Example: AND

• $x_1, x_2 in {0,1}$
• $y = x_1 text{AND} x_2$

We add the following weights to achieve the AND operation:

• $Theta_{10}^{(1)} = -30$
• $Theta_{11}^{(1)} = 20$
• $Theta_{12}^{(1)} = 20$

$h_Theta(x) = g(-30+20x_1+20x_2)$

$x_1$	$x_2$	$h_Theta(x)$
$0$	$0$	$g(-30) approx 0$
$0$	$1$	$g(-10) approx 0$
$1$	$0$	$g(-10) approx 0$
$1$	$1$	$g(10) approx 1$

Simple Example: OR

$h_Theta(x) = g(-10 + 20x_1 + 20x_2)$

$x_1$	$x_2$	$h_Theta(x)$
$0$	$0$	$g(-10) approx 0$
$0$	$1$	$g(10) approx 1$
$1$	$0$	$g(10) approx 1$
$1$	$1$	$g(30) approx 1$

Examples and Intuitition II

Negation

$h_Theta(x) = g(10 - 20x_1)$

$x_1$	$h_Theta(x)$
$0$	$g(10) approx 1$
$1$	$g(-10) approx 0$

XNOR

$x_1$	$x_2$	$a_1^{(2)}$	$a_2^{(2)}$	$h_Theta(x)$
$0$	$0$	$0$	$1$	$1$
$0$	$1$	$0$	$0$	$0$
$1$	$0$	$0$	$0$	$0$
$1$	$1$	$1$	$1$	$1$

Multiclass Classification

$y^{(i)}inmathbb{R}^n$ where $n$ is the number of classes.

$$h_Theta = left[begin{array}{c} 0 vdots 0 1 0 vdots 0 end{array}right]$$

The $i$-th column is equal to $1$ for the $i$-th feature of the output layer.

Advanced Optimization

With $j>1$ (note that octave indexes start at 1).

Neural Networks: Learning

Cost Function

$${ (x^{(1)}, y^{(1)}), …, (x^{(m)}, y^{(m)}) } L = text{number of layers in network} s_l = text{numbers of units (that are not bias units)}$$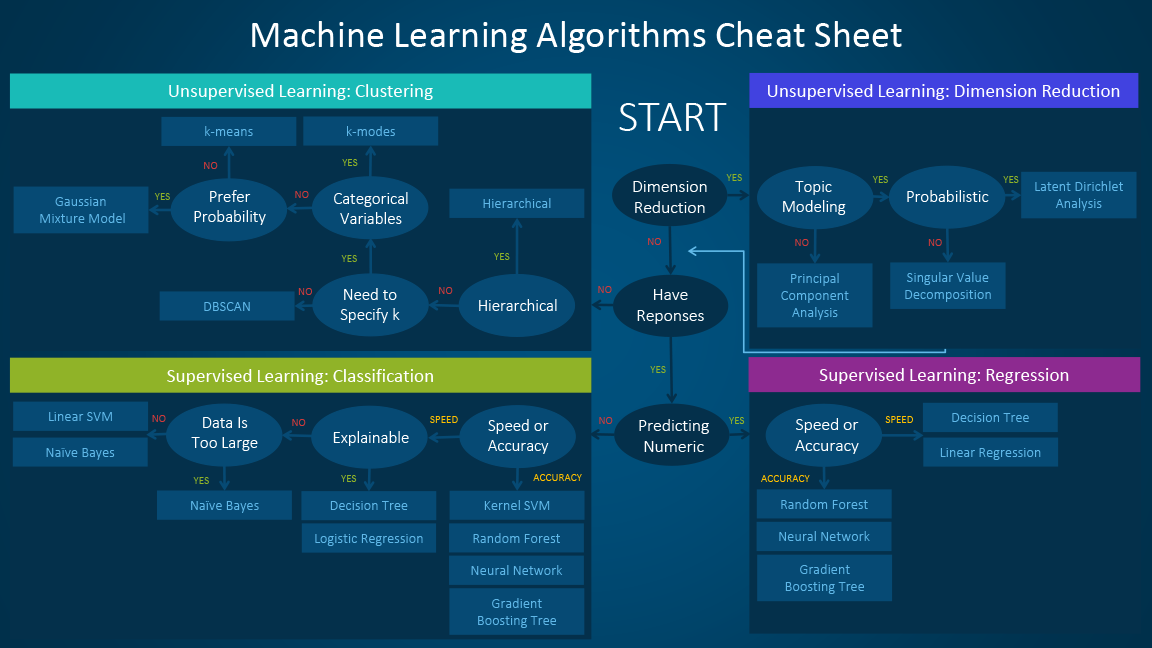

Binary Classification

$y in {0,1}$ with one output unit.

Multi-Class Classification

For $K$ classes: $y in mathbb{R}^K$ with $K$ output units.

Cost Function

The cost function for neural networks is similar to the regularized logistic regressions cost function.

$$ h_Theta(x) in mathbb{R}^K ;; (h_Theta(x))_i = text{i-th output} $$ $$begin{align} J(Theta) = &-frac{1}{m}left[ sum^{m}_{i=1} sum^{K}_{k=1} y^{(i)}_k log(h_Theta(x^{(i)}))_k + (1-y^{(i)}_k) log(1-(h_Theta(x{(i)}))_k) right] & + frac{lambda}{2m} sum^{L-1}_{l=1}sum^{s_l}_{i=1}sum^{s_{l+1}}_{j=1}(Theta^{(l)}_{ji})^2 end{align} $$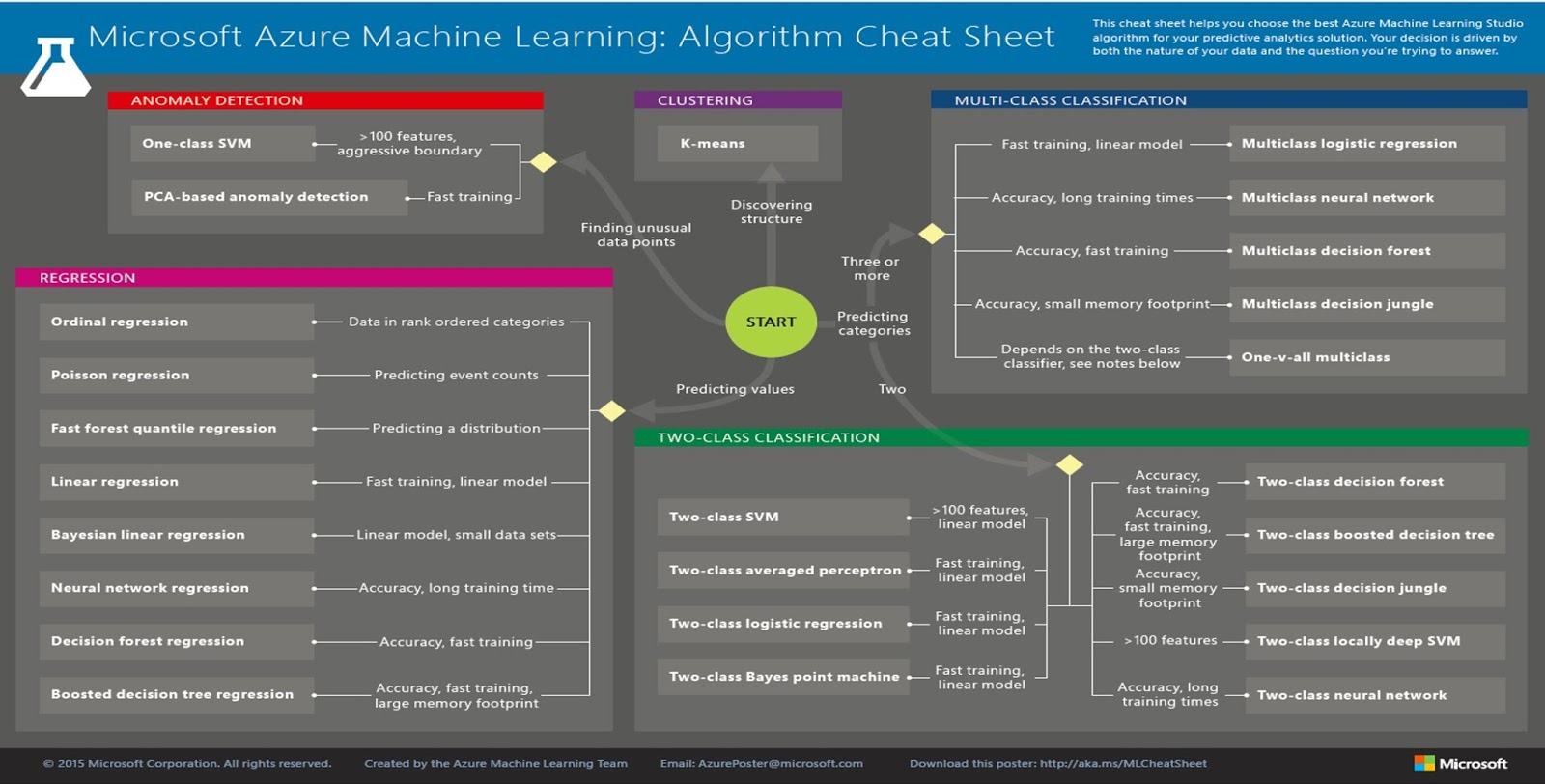

Backpropagation Algorithm

Gradient Computation

With $J(Theta)$ we now need $text{min}_Theta$. For that we need to compute:

• $J(Theta)$
• $frac{delta}{delta Theta^{(l)}_{ij}} J(Theta)$ with $Theta^{(l)}_{ij} in mathbb{R}$

Intuitition: $delta^{(l)}_j$ is the error of node $j$ in layer $l$. If we for example have a four layer network ($L = 4$) we have to calculate three errors:

• $delta^{(4)}_j = a^{(4)}_j - y_j$ what basically is $delta^{(4)} = h_Theta(x) - y$
• $delta^{(3)}_j = (Theta^{(3)})^T delta^{(4)} .* g'(z^{(3)})$
• $delta^{(2)}_j = (Theta^{(2)})^T delta^{(3)} .* g'(z^{(2)})$

Alrogithm: Backpropagation

The training set is :${ (x^{(1)}, y^{(1)}), ..., (x^{(m)}, y^{(m)}) }$. We now set $Delta^{(l)}_{ij} = 0 ; forall ; l,j,i$. $Delta$ is used to compute $frac{delta}{delta Theta_{ij}^{(l)}} J(Theta)$.

$$begin{aligned} text{for} ; & i = 1 ; text{to} ; m & text{set} ; a^{(1)} = x^{(i)} & text{perform forward propagation to compute} ; a^{(l)} ; text{for} ; l = 2,3,...,L & text{using} ; y^{(i)} text{, compute} delta^{(L)} = a^{(L)} - y^{(i)} & text{compute} ; delta^{(L-1)}, delta^{(L-2)}, ..., delta^{(2)} & Delta^{(l)}_{ij} := Delta^{(l)}_{ij} + a^{(l)}_j delta^{(l+1)}_i ;; text{(vectorized:} ; Delta^{(l)} = Delta^{(l)} + delta^{(l+1)} (a^{(l)})T ; text{)} D^{(l)}_{ij} &= frac{1}{m} Delta^{(l)}_{ij} + lambdaTheta^{(l)}_{ij} ;; text{if} ; neq 0 D^{(l)}_{ij} &= frac{1}{m} Delta^{(l)}_{ij} frac{delta}{delta Theta_{ij}^{(l)}} & J(Theta) = D^{(l)}_{ij} end{aligned}$$

Forward Propagation

$$text{cost}(i) = y^{(i)} log(h_Theta(x^{(i)})) + (1-y^{(i)})log(h_Theta(x^{(i)}))$$

The error of $a^{(l)}_{j}$ (unit $j$ in layer $l$) is:

$$delta^{(l)}_j = frac{delta}{delta z^{(l)}_j} text{cost}(i)$$

Implementation Note: Unrolling Parameter

Where gradient and theta are vectors in $mathbb{R}^{n+1}$.

If we have for example a neural network with four layers ($L=4$):

• $Theta^{(1)}, Theta^{(2)}, Theta^{(3)}$ are matrices (Theta1>, Theta2, Theta3)
• $D^{(1)}, D^{(2)}, D^{(3)}$ matrices (D1, D2, D3)

all unrolled into vectors.

Example

$$s_1 = 10, s_2 = 10, s_3 = 1 Theta^{(1)} in mathbb{R}^{10x11}, Theta^{(2)} in mathbb{R}^{10,11}, Theta^{(3)} in mathbb{R}^{1x11} D^{(1)} in mathbb{R}^{10x11}, D^{(2)} in mathbb{R}^{10,11}, D^{(3)} in mathbb{R}^{1x11} $$

Learning Algorithm

• Have initial parameters $Theta^{(1)}, Theta^{(2)}, Theta^{(3)}$
• Unroll to get initialTheta to pass to fminunc(@costFunction, initialTheta, options)

function[jVal, gradientVec] = costFunction(thetaVec)

• From thetaVec, get $Theta^{(1)}, Theta^{(2)}, Theta^{(3)}$ via reshape
• Use forward/backward propagation to compute $D^{(1)}, D^{(2)}, D^{(3)}$, unroll to get gradientVec

Gradient Checking

$$frac{d}{dJ(theta)} = frac{J(theta + epsilon)- J(theta - epsilon)}{2epsilon}$$

with $epsilon = 10^{-4}$. The implementation would look like this:

The parameter vector $theta mathbb{R}^n$ is the unrolled version of all the $Theta^{(l)}$. The partial derivitives of the cost function would look like this:

$$frac{delta}{delta theta_1} J(theta) = frac{J(theta_1 + epsilon, theta_2, ..., theta_n) - J(theta_1 - epsilon, theta_2, ..., theta_n)}{2 epsilon} frac{delta}{delta theta_2} J(theta) = frac{J(theta_1, theta_2 + epsilon, ..., theta_n) - J(theta_1, theta_2 - epsilon, ..., theta_n)}{2 epsilon} ... frac{delta}{delta theta_n} J(theta) = frac{J(theta_1, theta_2, ..., theta_n) + epsilon - J(theta_1, theta_2, ..., theta_n - epsilon)}{2 epsilon} $$

We then need to check that gradApprox $approx$ DVec returned from the back propagation.

Implementation Note

• Implement the back propagation to compute DVec (unrolled $D^{(1)}, D^{(2)}, D^{(3)}$)
• Implement numerical gradient checking to compute gradApprox
• Make sure they have similar values
• Turn off gradient checking. Using backprop code for learning.

Important: Be sure to disable gradient checking before training your classifier. If you run numerical gradient computation on every iteration of gradient descent your code will be very slow.

Random Initialization

For gradient descent and advanced optimization method, we need an initial value for $Theta$.

Consider gradient descent with initialTheta = zeros(n,1).

Zero Initialization

When initialized with zero, after every update the parameters corresponding to the inputs going into each of the hidden units are identical.

Random Initialization: Symmetry Breaking

Initialize each $Theta^{(l)}_{ij}$ to random value in $[-epsilon, epsilon]$. For example:

Putting it together

• Pick a network architecture (connectivity pattern between neurons)
• Number of inputs: dimensions of features $x^{(i)}$
• Number of output units: number of classes

(Reasonable default: one hidden layer, or if more than one hidden layer, you need to have the same number of hidden units in every hidden layer (usually the more the better))

Training a Neural Network

• Randomly initialize weights
• Implement forward propagation to get $h_Theta(x^{(i)})$ for any $x^{(i)}$
• Implement code to compute cost function $J(Theta)$
• Implement back propagation to compute partial derivitives $frac{delta}{delta Theta^{(l)}_{jk}} J(Theta)$

  For all features:

  • Perform forward and backward propagation using the example $(x^{(i)}, y^{(i)})$
  • (Get activations $a^{(l)}$ and delta terms $delta^{(l)}$ for $l=2,…,L$)
  • Compute partial derivitive of the cost function
• Use gradient checking to compare $frac{delta}{delta Theta^{(l)}_{ij}} J(Theta)$ computed using backpropagation vs. using numerical estimate of gradient of $J(Theta)$. Turn off code for gradient checking.
• Use gradient descent or adavanced optimization method with backpropagation to try to minimize $J(Theta)$ as a function of parameters $Theta$

Week 5

Deciding What to Try Next

Debugging a learning algorithm

Suppose you implemented regularized linear regression. However, when you test your hypothesis on a new set of data, you find that it mameks unacceptably large errors in its predictions. What should you try next?

• Get more training examples
• Try a smaller set of features
• Try getting additional features
• Try adding polynomial features
• Try decreasing $lambda$
• Try increasing $lambda$

Machine Learning Diagnostics

Machine Learning Algorithms Cheat Sheet Free

Diagnostic: A test that you can run to gain insight what is/isn't working with a learning algorithm, and gain guidance as to how best to improve its performance.

Diagnostics can take itme to implement, but doing so can be very good use of your time.

Evaluating a Hypothesis

To test the hypothesis, the training data gets split into a training set (bigger part) and a test set (smaller part). You could for example split them into 70%/30%. Note that the data is sorted, the picks should be randomized, or the data should be randomly shuffled.

• Training set: $$begin{array}{c} (x^{(1)},y^{(1)}) (x^{(2)},y^{(2)}) vdots (x^{(m)},y^{(m)}) end{array}$$
• Test set (with $m_text{test}$: number of examples): $$begin{array}{c} (x^{(1)}_text{test},y^{(1)}_text{test}) (x^{(2)}_text{test},y^{(2)}_text{test}) vdots (x^{(m)}_text{test},y^{(m)}_text{test}) end{array}$$

Training/Testing Procedure for Linear Regression

Learn parameter $theta$ from training data (minimizing training error $J(theta)$ and compute the test set error:

$$ J_text{test}(theta) =frac{1}{2m_text{test}} sum^{m_text{test}}_{i=1} left( h_theta(x^{(i)}_text{test} - y^{(i)}_text{test}) right) $$

The misclassification error:

$$text{err}(h_theta(x), y) = left{begin{array}{l} text{if} ; h_theta(x) geq 0.5 ;; y=0 text{or if} ; h_theta(x) lt 0.5 ;; y=1 end{array}right.$$

The test error is:

$$frac{1}{m_text{test}} sum^{m_text{test}}_{i=1} text{err}(h_theta(x^{(i)}_text{test}), y^{(i)}_text{test})$$

Model Selection and Train/Validation/Test Sets

Once parameters $theta_0, theta_1, cdots, theta_4$ were fit to some data (training set), the error of the parameters as measured on that data (the training error $J(vectheta)$) is likely to be lower than the actual generalization error.

Model Selection

1. $h_theta(x) = theta_0 + theta_1 x$ with $d=1$ $rightarrow$ $Theta^{(1)} rightarrow J_text{test}(Theta^{(1)})$
2. $h_theta(x) = theta_0 + theta_1 x + theta_2 x^2$ with $d=2$ $rightarrow$ $Theta^{(2)} rightarrow J_text{test}(Theta^{(2)})$
3. $h_theta(x) = theta_0 + theta_1 x + theta_2 x^2 + theta_3 x^3$ with $d=3$ $rightarrow$ $Theta^{(3)} rightarrow J_text{test}(Theta^{(3)})$
4. …
5. $h_theta(x) = theta_0 + theta_1 x + cdots + theta_10 x^10$ with $d=10$ $rightarrow$ $Theta^{(10)} rightarrow J_text{test}(Theta^{(10)})$

In order to select a model you could take the hypothesis with the lowest test set error. (Let's say for now it's $theta_0 + cdots + theta_5x^5$). Now how well does it generalize? report the test set error $J_text{test}(theta^{(5)}$

Machine Learning Algorithms Cheat Sheet R

The problem is, that $J_text{test}(theta^{(5)}$ is likely to be an optimistic estimate of generalization error, i.e. our extra parameter ($d$ = degree of polynomial) is fit to the test set.

Now instead of splitting it 70/30 we split the dataset like this: 60% training set, 20% cross validation set ($cv$) and 20% test set.

• $$begin{array}{c} (x^{(1)}, y^{(1)}) (x^{(2)}, y^{(2)}) vdots (x^{(m)}, y^{(m)}) end{array}$$
• $$begin{array}{c} (x^{(1)}_{cv}, y^{(1)}_{cv}) (x^{(2)}_{cv}, y^{(2)}_{cv}) vdots (x^{(m)}_{cv}, y^{(m)}_{cv}) end{array}$$
• $$begin{array}{c} (x^{(1)}_{text{test}}, y^{(1)}_{text{test}}) (x^{(2)}_{text{test}}, y^{(2)}_{text{test}}) vdots (x^{(m)}_{text{test}}, y^{(m)}_{text{test}}) end{array}$$

Where $m_{cv}$ is the number of cross validation examples.

Machine Learning Algorithms Cheat Sheet 5th

• Training error: $J(theta) = frac{1}{2m} sum^{m}_{i=1} (h_theta(x^{(i)})-y^{(i)})^2$
• Cross Validation error: $J_{cv}(theta) = frac{1}{2m_{cv}} sum^{m_cv}_{i=1} (h_theta(x^{(i)}_{cv})-y^{(i)}_{cv})^2$
• Cross Validation error: $J_{text{test}}(theta) = frac{1}{2m_text{test}} sum^{m_text{test}}_{i=1} (h_theta(x^{(i)}_{text{test}})-y^{(i)}_{text{test}})^2$

Now to select a model you calculate $min_theta J(theta)$ for $theta^{(i)}$ and then calculate $J_{cv}(theta)$. You then select the model with the lowest cross validation error.

Diagnosing Bias vs. Variance

Suppose your learning algorithm is performing less wellt han yoh were hoping. ($J_{cv}(theta)$ or $J_text{test}(theta)$ is high.) Is it as bias problem or a variance problem?

• Bias (underfit): $J_text{train}(theta)$ will be high, $J_{cv}(theta) approx J_text{train}(theta)$
• Variance (overfit): $J_text{train}(theta)$ will be low, $J_{cv}(theta) gtgt J_text{train}(theta)$

Regularization and Bias/Variance

Machine Learning Algorithms Cheat Sheet Pdf

Linear Regression with Regularization

Choosing the Regularization Parameter $lambda$

Full Cheat Sheet On Machine Learning Algorithms In Python And R Pdf

Bias/Variance as a Function of the Regularization Parameter $lambda$

Learning Curves

Appendix

Footnotes

1. Taken from the Machine Learning Video Lecture: »What is Machine Learning?«, Minute 01:49 at Coursera